国外号称原版的《几何原本》是如何发现的？

1897年，两名来自英国牛津大学的学生，闲得没事，专门跑到埃及亚明省俄克喜林库斯市的郊外去翻露天垃圾堆。注意，是露天垃圾堆。

冥冥之中，仿佛有什么召唤似的，不远千里，必有所得。

结果也毫不意外，他们真的就在垃圾堆中有了“旷古绝今”的巨大发现，翻出了超过50万张的莎草书碎片，其中包括欧几里得《几何原本》残篇。

这种翻垃圾堆似的“发现”就像天上掉馅儿饼，一去一个准，绝没有空手而回的道理。

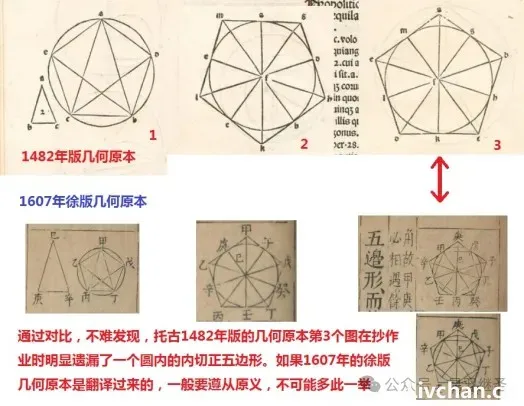
正因为如此，在1482年、1574年、1607年徐版三个《几何原本》中比对研究，发现一些问题，就很正常了。

几何原本不同版本的比较分析

首先，1574年的拉丁文版《几何原本》第153页中出现了“欧几里得”（原文:Verum Euclides de sola Geometrica agit in hoclibro，大意为：欧几里得的真理，是唯一的几何学真理），但是在徐光启版本的《几何原本》中却只字未提。

如果《几何原本》真是出自欧几里得之手，利玛窦和徐光启又是翻译过来的，这二人怎么可能忘了原作者，对其只字不提呢？

更有意思的是，第153页中还出现了“Arithmetica”这个单词，其词源如前文《推倒历史重来：若要天翻地覆，就让它天翻地覆》所述，与华夏有着千丝万缕的关系。

其次，1574年拉丁文版的《几何原本》中出现了“Geometrica”一词，如前文《《几何原本》的作者果真是两个中国人，呵呵！》所述，由于Geo一词最早是在1631年由传教士艾儒略创造，所以时间上产生了矛盾，这也证明1574年的拉丁文版《几何原本》系伪造。实际上，下文考证的结果将会显示，Geometry一词的诞生极有可能大大晚于1631年，其真实的创造者应为1822年的马礼逊。

此外，笔者将1574年拉丁文版的《几何原本》第153页与第一部可读的拉丁文《几何原本》、1482年由Erhard Ratdolt出版的版本进行比较，发现在1482年的版本中遍寻不着“proportio vero est rationum similitudo”（相似比例是真实的比例）这部分内容，1482年版本表述的比例是在用“随意画就”的横向线段。两相对比，显然1574年的版本已经是经过西人在后世增补和修改的了，并非出自欧几里得之手。实际上，1482年版本的几何原本仅有284页，而1574年的版本则有1356页。将1482年、1574年、1607年三个版本的几何原本放在一起比较，会发现有关“比例”方面的内容、所举例子的数值等并不完全相同。

（1482年版本的几何原本，没有页码显示）

（1482年版本的几何原本，没有页码显示）

（1574年版本的几何原本，有页码显示）

（几何原本，明万历三十五年即1607年.初刊本）

经过比较研究，需要指出的是，1574年版本第153页内容中，所谓的拉丁文单词“Proportio”就是英语单词“Proportion”（比率）去掉一个n后得来，查阅1836年新英拉简明安斯沃思字典《A new abridgment of Ainsworth's dictionary，English and Latin》第274页可知，直到1836年该词的解释仍旧是“Measure,comparison”(测量、比较），尚未形成“比率、比例”的数学含义。所以，1574年用这样一个没有“比例”含义的单词来表示数学含义——比例，本身就已经说明了问题。

1482年版的几何原本也存在上述问题，以及一些其他问题。以下图为例，举例说明：

1）行文中多次提及“Proportio”这个拉丁语单词，用它来表示“比例”的含义，然而，1836年的拉丁语英语字典中该词只有“测量、比较”的含义，仍旧没有“比例”的数学含义；

2）左侧两图表式的比例有倍乘关系，但线段与数量的对应关系根本不成比例，数量混乱、逻辑混乱；

3）1607年徐版几何原本中没有与之对应的内容，说明徐版几何原本与1482年几何原本存在不同。其实，1482年版几何原本中还有不少内容与徐版几何原本不同，许多图“巧作繁饰”，一开始就故意画得很复杂，不像徐版几何原本是由浅入深，从简单到复杂，循序渐进，而且，前述复杂的图案及描述内容，在徐版几何原本中也找不到对应内容。

如果徐版几何原本是从国外翻译过来的，那为什么1482年的这些内容却偏偏漏掉，而不翻译呢？

（1482年版本的几何原本，没有页码显示）

通过对数学史比例的形成研究，可以确定比例的概念大致在明朝晚期发展成熟，明末李之藻著《圜容较义》（四库全书本，第9-10页）第五题中明确提及了比例：

“凡直角三边形，任将一锐角于对边作一直线分之，其对边线之全与近直角之分之比例大于全锐角与所分内锐角之比例。”

需要明确指出的是，此书为李之藻所著，与网上流传的利玛窦传授的说法无关。

巧的是，徐光启所著《测量法义》（四库全书本，第17-18页）天文算法类一“本题十五首”中也阐述了比例的内容，说明徐光启对比例的概念非常熟悉：

“如在直景乙戊，得八度正庚辛景三十步，即以表度十二庚辛三十步相乘，得三百六十为实，以乙戊八度为法，除之，得四十五，即己庚之高四十五步。

若权线在倒景边，即景大于物，本篇三题注。则表与倒景之比例若物之景与其高，用三数法。以表为第一数，以倒景上所值度分为第二数，以物景之度为第三数，算之，即所得数为其物高。”

同样需要指出的，这本《测量法义》是徐光启所撰，与利玛窦也没有任何关系。所以，徐光启将明朝末年发展成熟的“比例”写入《几何原本》是完全可能的。

但是，1482年和1574年的几何原本中出现有关“比例”的成熟概念，却有些不合时宜，因为一不小心就穿越了，把后世产生的概念写到几百年前的版本中，这样的把戏一旦被识破，岂不是致命的漏洞？更何况西史宣称《几何原本》诞生于两千多年前的古希腊时代。两千多年前的古希腊时代，比例的概念尚未诞生，又如何能写入《几何原本》呢？

通读1607年徐版《几何原本》，还可以发现一个基本事实：明人徐光启在书中从未使用过清人李隐山于1679年独创的内切圆正五边形和十边形画法。

然而，令人啧啧称奇的是，这个1679年才出现的作图法却神奇般地出现在了1574年的几何原本（第143页）中。也就是说，再此发生了穿越事件。

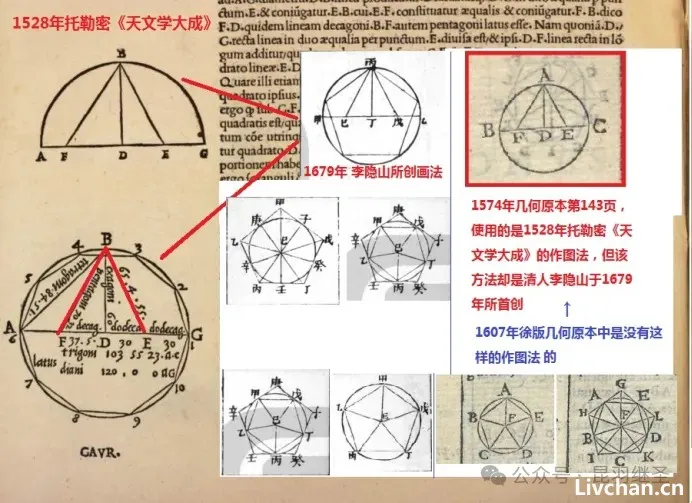
托古1482年的几何原本中，使用的是徐版几何原本的作图法，这个方法与清人李隐山的画法是有差别的。

通过对比，不难发现，托古1482年版的几何原本第3个图在抄作业时明显遗漏了一个圆内的内切正五边形。如果1607年的徐版几何原本是翻译过来的，一般要遵从原义，不可能多此一举，自作主张去添加一些其他图案。

关于几何原本的译名

在1822年马礼逊《华英字典》第347页有一个单词Quantity，该单词的解释只有“几多”、“多少”、“若干”，而没有别的意思。在这里，出现了“几何原本”几个大字。

彼时，几何原本被译为：

“Quantity（or the measurement of it）the principles of.”

这是典型中式语法，若按现在的理解，应表述为“the principles of Quantities”，说明当时的英语语法还很稚嫩，尚未成熟。

Quantity 对应“几何”；“（or the measurementg of it）the principles of”对应“原本”，从字面意思上来理解，其实就是“测量的法则”。

笔者对此有个很大的疑问。如果《几何原本》真如西方所言，是古希腊的欧几里得所著，传承了几千年，鉴于其重要性和在西方的大名，那么，它的西文名称必然是确定的、唯一的（只要有书存世，书上印刷的名称一定是固定的），绝对不可能出现多个西文名称，还无法对应起来的情况。

按现行西史，几何原本的英文名称为Euclid's Elements，若按字面意思翻译，应该是“欧几里得的元素”；若按意译，可为“几何原本”。前述二者“欧几里得的元素”和“几何原本”，是翻译成中文后出现的两个名称，一个直译，一个意译，因此存在差异，但是二者锚定的原型都是同一个，即“Euclid's Elements”，没有第二个英文名称。

作为一个学识丰富的英国伦敦会传教士，马礼逊肯定接触、甚至认真学习过几何原本，那他对于几何原本的西文名称应该十分熟悉才对，怎么会如此拙劣地弄错几何原本的名称，把它翻译为“Quantity（or the measurement of it）the principles of.”呢？

这无论如何说不过去。

实际上，马礼逊是真不知道几何原本那个固定、确定、唯一的西文名称，他在1822年《华英字典》第187页解释“Geometry”时，有这么一段话：“the principles of geometry  and trigonometry,as explained in geometrical figures几何原本 the principles of quantity .”

翻译过来，大意为“大地测量和三角学的规则，陈述于地理算术中”。

不过，由于这个解释无法涵盖几何原本的全部含义，马礼逊又不得不在上述这段话后补充了一句“the principles of quantity”（数量的法则）。换言之，由于几何原本和中文博大精深，马礼逊在翻译名称时就碰到了巨大的挑战和困难，只能多翻译些名称，留待西方后人去确定。对于马礼逊本人而言，他个人是倾向于使用“the principles of quantity”（数量的法则）作为几何原本的西文名称的。假如几何原本源自西方，那它的名称就应该是固定的，不会出现这种翻译困难和选择困难。

另外，在第187页Geometry的上面有一个英语单词Geomancy，其解释为“风水”、“风水先生”、“堪舆先生”，带着浓厚的华夏色彩，说明以Geo（几何）这个词根与中国存在着千丝万缕的关系。

关于Geometry一词的解释，其演变如下：

1812年斯蒂芬·琼斯《英语通用发音解释词典》（《A General Pronouncing and Explanatory Dictionary of the English Language》第173页中，其解释为：

“the science of quantity,extension,or magnitude abstractedly considered.”

大意：

“抽象考虑数量、外延或量级的科学”。

1816年威廉姆·恩菲尔德在伦敦出版的《通用发音词典》（《A General Pronoucing Dictionary）第123页，对Geometry的解释与1812年的上述解释相同，也是“the science of quantity, extension, or magnitude abstractedly considered.”（抽象考虑数量、外延或量级的科学）。

令人疑惑的是，既然1812年和1816年对Geometry 已经有了“详细的解释”，为什么1822年的马礼逊在注释Geometry时却不知道1812年和1816的含义，以至于完全没有继承其原解释？

对此现象，最合理的解释其实只有一个，那便是很可能是马礼逊“创造”了Geometry这个单词，并将其用于几何原本的名称翻译，但是具体的定义，马礼逊当时并没有想好。

而1812年、1816的英语字典由于本身内容涉伪，是大约在19世纪中期伪造“英语历史悠久和发展脉络”的一种产物，所以用后世拟定的枯燥抽象术语去套在以前的单词头上并不稀奇。

不仅马礼逊不知道1812年、1816年Geometry的定义，而且麦都思、罗存德也都不知道，这就很说明问题了。

1847年，麦都思《汉英字典》第621页，对Geometry的解释是“丈量地法”，与1812年、1816年Geometry的解释大相径庭，但更贴近实际，容易理解。在本页中，麦都思放弃了马礼逊倾向于使用的“the principles of Quantity”作为几何原本的西文名称，而是截取马礼逊在解释Geometry时的前面四个单词“the principles of Geometry”、同时舍弃后面的部分（即and trigonometry,as explained in geometrical figures），将其作为几何原本的西文定名。

于是乎，几何原本的名称，就变成了“the principles of Geometry”。

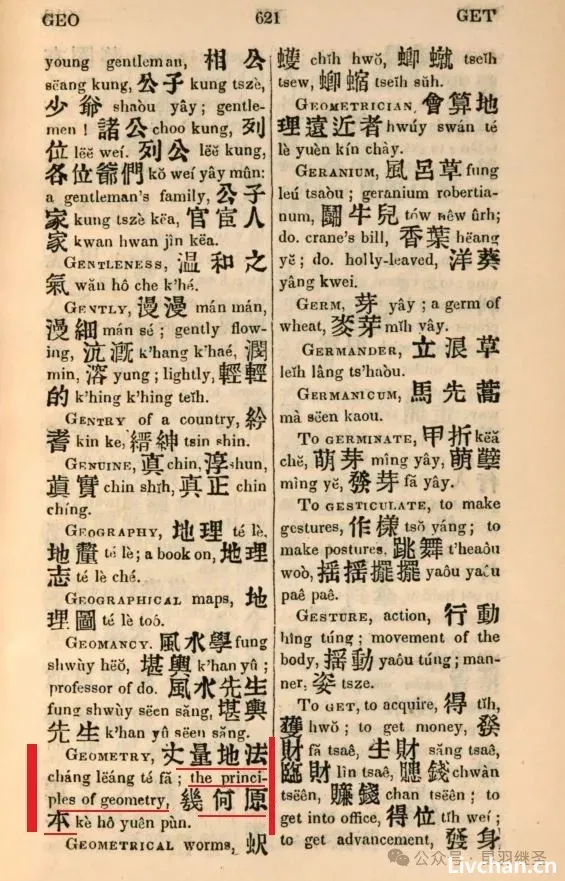
1867年，罗存德《英华字典》第893页，继承了麦都思对几何原本的名称翻译“the principles of geometry”，而且明确注明这是“量地之理”。也就是说，西人对几何原本的理解，就是“量地之理”，几何原本等于量地之理。

令人感到惊异的是，1844年《关于所有时代和国家的海顿通用词典》（Dictionary of dates and universal reference, relating to all ages and nations）中，第230页对 Geometry 有这么一段描述，里面却明确提到了“几何原本”的西文正式名称“Euclid's elements”：

“GEOMETRY. Its origin is ascribed to the Egyptians ; the annual inundations of the Nile having given rise to it by carrying away the landmarks, and the boundaries of farms. Thales introduced geometry into Greece about 600 B.C. Euclid's elements were compiled about 280 B.C. The doctrine of curves originally attracted the attention of geometricians from the conic ps, which were introduced by Plato aboat 390 B.C. The conchoid curve was invented by Nicomedes, 220 B.C. The science of geometry was taught in Europe in the thirteenth century. Books on the subject of geometry and astronomy were destroyed in England, being regarded as infected with magic, 7 Edward VI., 1552.-Stowe.”

大意：

“几何学。它的起源归功于埃及人；尼罗河每年的洪水尼罗河冲毁了地标和农场的边界，导致土地流失。泰勒斯在公元前 600 年左右将几何学引入希腊。欧几里德在元始前 280 年左右编写了《几何原本》。曲线原理最初吸引了几何学家的注意力，他们研究了圆锥曲线。柏拉图在元始前 390 年左右引入了圆锥曲线。尼科梅德斯在元始前 220 年左右发明了螺形曲线（即尼科梅德斯蚌线）。13 世纪，欧洲开始教授几何学。1552 年，爱德华六世下令摧毁几何学和天文学书籍，称其与巫术有关。”

既然西方有几何原本的正式名称，那为什么博学多闻的马礼逊、麦都思、罗存德都不知道？这几位在西方历史中可都是著述颇丰的大能级人物啊。

笔者还注意到一个随意篡改的地方。

在1844年海顿字典上述内容中，宣称的是“欧几里德在元始前 280 年左右编写了《几何原本》”，然而，现行西史却称，大约在元始前300年，欧几里得比较系统地总结了古代劳动人民长期积累的几何知识，把人们公认的一些事例归纳成定义和公理，用它来研究图形的性质，写成了《几何原本》一书。

这二者之间存在时间差异，相差了大约20年。

1866年《关于所有时代和国家的海顿通用词典:第十二版》（Haydn's Dictionary of dates, relating to all ages and nations for universal reference, twelfth edition）中，第333页对Geometry的解释发生了改变，不但将欧几里得几何原本的成书时间从元始前280年修改为元始前300年，还增加了如下内容：

“so termed from its original applicaion to measuring the earth……Simon's celebrated edition of Euclid first appeared in 1756.”

大意：

“从最初的应用到测量大地……西蒙的著名欧几里得版本于1756年首次出现。”

显然，此处增加的“测量大地”，便是1847年麦都思《汉英字典》中提及的“丈量地法”。而所谓的1756年西蒙的著名欧几里得版本，则是后世杜撰的内容。

1870年《关于所有时代和国家的海顿通用词典》（Haydn's Dictionary of dates, relating to all ages and nations for universal reference）中，第330页在对Geometry进行解释时，又添油加醋地虚构了一堆内容，以前从未出现过的阿基米德、托勒密、笛卡尔、牛顿，悉数出现了：

“Archimedes, a discover in geometry, 287-212 B.C. …… Ptolemy, the astronomer, （A.D.）2nd century. …… Descartes published his Analytical Geometry, 1627. Sir Isaac Newton （Arithmetica Universalis, &.） 1642-1727. ”

大意：

“阿基米德，几何学的发现，元始前287-212年……天文学家托勒密，（元始）2世纪……笛卡尔于1627年出版了《分析几何》。艾萨克·牛顿爵士（《广义算术》）1642-1727年。”

原来，上述内容都是1870年编造出来的，此前的记载中并没有。

有意思的是，此处编造的牛顿生卒年是1642-1727年，而现行西史宣称的却是1643-1727年。

1873年《关于所有时代和国家的海顿通用词典：第十四版》（Haydn's Dictionary of dates, and universal information relating to all ages and nations : fourteenth edition）第305页，又编造了毕达哥拉斯、拉普拉斯的新内容，并再次重提尼科梅德斯蚌线：

“Pythagoras cultivated the science about 580. …… The conchoid curve invented by Nicomedes, 220 B.C. ……La Place's Mecanique Celeste, 1799-1805. ”

大意：

“毕达哥拉斯在580年左右培育了科学……尼科梅德斯于元始前220年发明的螺形曲线（即尼科梅德斯蚌线）……拉普拉斯《天体力学的新方法》（Les Methodes Nouvelles de la Mecanique Celeste），1799-1805年。”

而后，上述内容就定型，一直保持到了1910年，再延续到了现在。

实际上，即便是Element一词，也与华夏存在密切关联。

1822年马礼逊《华英字典》第138页，对Element的解释为中国五行，即“金水木火土”。所以，几何原本的西文名称“Euclid's elements”，按照彼时的字面意思翻译过来就是“欧几里得的中国五行金水木火土”，这与数学上的几何学可谓“风马牛不相及”。

1847年，麦都思在编撰成书的《英汉字典》第一册第486页中，继承了马礼逊对 Element 的定义，保留了“五行”、“金水木火土”的解释，但将其位置往后挪了挪，并着手添加了其他解释，如“元质”、“元行”、“四元”等等。麦都思将中国先天概念、源初概念之“元”，即“元气”之“元”，用于解释Element，并赋予其“最初主要物质”的含义。

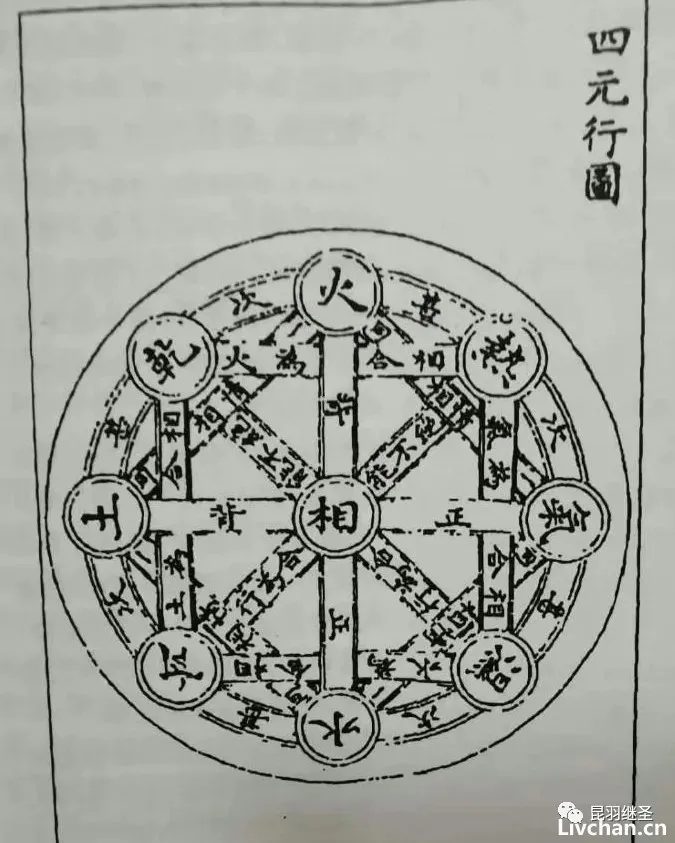
需要指出的是，麦都思在这里特意添加的“四元”解释，源自利玛窦《乾坤体义》中的四元行论，——这是在为弱化中国五行、用西方四行来解释Element做准备。后面再把“四行”改成“四元素”，这样与华夏之间的联系从表面上就看不出来了。

利玛窦提出的四元行论，后来还真被改成了“四元素”学说。不过，万变不离其宗，利玛窦宣称万物皆由火、气、水、土四种元素构成，竟然与佛经几乎完全相同（而佛经的这个学说，恰好又来源于五行）。

利玛窦在《乾坤体义》中言称：

“天下凡有形者，俱从四行成其质，曰火、气、水、土是也，其数不可阙增也。夫行之本情，并为四也，曰热、干、冷、湿是也。四元行，每二元情配合为性而成焉。若冷与热，干与湿，直相背而不可同居，以为二行矣。”

佛经常言“四大皆空”，那么，是哪四大呢？

这四大便是“地、水、火、风”，此为构成万物的四种基本元素，协助利玛窦抄录编书的人耍了个小聪明，把“地”换成“土”，把“风”改成了“气”，然后，就变成西方的宝贝疙瘩——四元行论了。

1867年罗存德《英华字典》第713页，在对Element进行解释时，“金水木火土”这种特别明显的字眼被刻意删除，“五行”的解释虽然予以保留，但位置愈发靠后，已经快要淹没在一大堆解释中了。不仔细看的话，还真不容易发现那小小的“五行”二字。

Element的解释，为什么会将“元”、“本”（本质的本）排在首位呢？

因为Ele-ment本身就是对“元”和“本”的记音造词，Ele发音近似「一额恩」连读 → 元，ment 发音则近似 “本”。

当1847年英国伦敦会传教士麦都思改造Element一词的解释，把利玛窦“四元”概念加入其中后，1857年，接手的伟烈亚力授意李善兰增补几何原本后9卷时，便琢磨起了几何原本正式的西文名称。

1857年《几何原本》第81页，有两页夹在当中的英文，标题为“Translation of Euclid's elements”，可译为“欧几里得几何原本的翻译”，又或“欧几里得元素的翻译”。

在这一页，传教士伟烈亚力称，《几何原本》的最初译名是“Elements of (the science) of Quantity (or so much)  ”，这个是伪造的“拼凑译名”：

1）Element，源自于1822年马礼逊《华英字典》，并经1847年麦都思《英汉字典》改造；

2）the science of Quantity，是截取了1812年、1816年两本英语字典中对Geometry的前面一部分解释。恰好，马礼逊早期倾向于使用“the principles of quantity”来表述《几何原本》，二者都有Quantity。

从几何原本的名称演变来看，西文名称多有变化，只有中文名称“固定不变”，这正好符合了翻译的正常逻辑——翻译可以有多种，但唯有原型、原本不会改变，这么多年来，中文几何原本还有什么别的名称吗？

那封面上的书名，早已确定，岂可擅自修改？

这不恰恰说明，几何原本出自华夏，中文版才是真正的底本？

若按《几何原本》最初译名“Elements of (the science) of Quantity (or so much)  ”，根据1822年马礼逊《华英字典》对Element的解释“中国五行”，则该译名应为——“中国五行的科学数量”！

来源：昆羽继圣